

Thus the following two functions are possible PDFs.
CDF AND PDF PDF
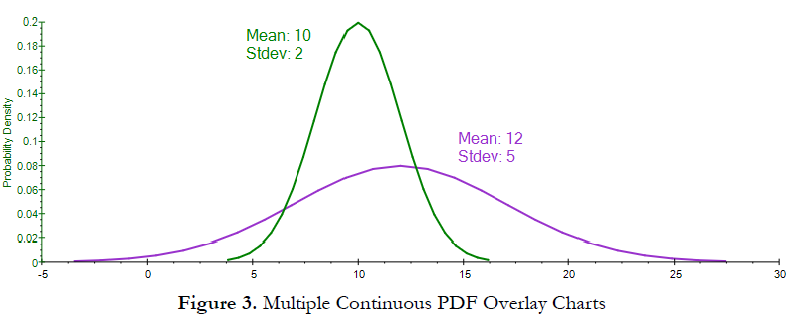
The exponential, Weibull and other distributions have PDFs defined, yet it is possible to have an arbitrary function meet the requirements of a PDF. Probability Density Function (PDF) vs Cumulative Distribution Function (CDF) The CDF is the probability that random variable values less than or equal to x whereas the PDF is a probability that a random variable, say X, will take a value exactly equal to x. Another property is the PDF is defined across the entire sample space. The PDF also has the property that the area under the curve for is one. Like a histogram, the PDF when plotted reveals the shape of the distribution.
CDF AND PDF ISO
Risk Management Using ISO 31000 Course Landing Page.14 Ways to Acquire Reliability Engineering Knowledge.Reliability Engineering Management DRAFT.Innovative Thinking in Reliability and Durability.Equipment Risk and Reliability in Downhole Applications.The CDF is the integration, from left to right, of the PDF. Musings on Reliability and Maintenance Topics The probability density function (PDF) and cumulative distribution function (CDF) help us determine probabilities and ranges of probabilities when data follows a normal distribution.Metals Engineering and Product Reliability.Product Development and Process Improvement.Rooted in Reliability: The Plant Performance Podcast.It is a probability of hitting infinitesimal (infinitely small) interval $$ when throwing a dice with infinite number of walls. You can easily notice that it changes as the range between $a$ and $b$ (i.e the total area) changes, it is nicely described in Can a probability distribution value exceeding 1 be OK? thread. Simple example is continuous uniform distribution with minimum of $a$ and maximum of $b$, where probability density is the same for each $x$ and equal to This leads us to defining probability density as "probability per foot". Probability mass function has no sense for continuous random variables since $\Pr(X=x)=0$ for continuous random variables (check also Why X=x is impossible for continuous random variables?), because simply a point on real line is so "small" that has no mass and no area. In dice case it's probability that the outcome of your roll will be exactly $x$. Probability density function (PDF) is a continuous equivalent of discrete probability mass function (PMF). In dice case it's probability that the outcome of your roll will be $x$ or smaller. The definition is the same for both discrete and continuous random variables. Text is consulted, the term may refer to:Ĭumulative distribution function (CDF) is sometimes shortened as "distribution function", it's To define a particular probability distribution. As noted by Wikipedia, probability distribution function is ambiguous term:Ī probability distribution function is some function that may be used


 0 kommentar(er)
0 kommentar(er)
